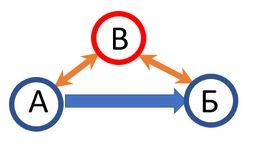
Как уже было отмечено, использование коммуникаций peer-to-peer (p2p) фактически лишает участников коммуникаций правовой защиты, так как юридическая значимость это всегда в той или иной форме свидетельство третьего не аффилированного лица. Счастливой особенностью ИТ является возможность свидетельства путем регистрации хэшкодов без необходимости предъявлять свидетелю содержание фиксируемого документа.

Таким образом, в среде юридически значимых коммуникаций любая транзакция между абонентами А и Б должна быть исполнена с привлечением в качестве свидетеля уполномоченного на то участника С. При этом оба абонента должны получить от С подтверждение факта фиксации транзакции. И так, любая транзакция, чтобы она имела правовую защиту должна выполняться в треугольнике типа А-С-Б.

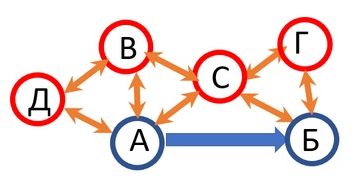
Но неаффилированность любой пары участников не может быть доказана. Абонент А может опасаться сговора Б с С. Чтобы в такой ситуации иметь защиту, абонент А должен привлечь к фиксации транзакции А-С свидетеля В. Аналогично Б, опасаясь сговора А и С привлекает к фиксации транзакции Б-С свидетеля Г. Но транзакция А-В тоже должна иметь свидетеля Д... В принципе, такая рекурсия может быть бесконечной и ограничиваться только степенью паранойи участников.

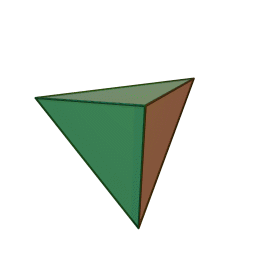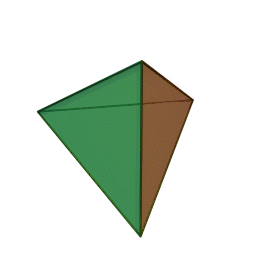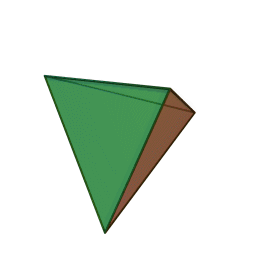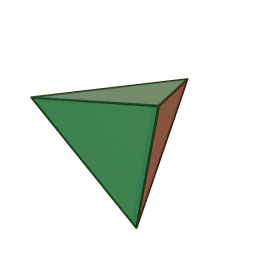
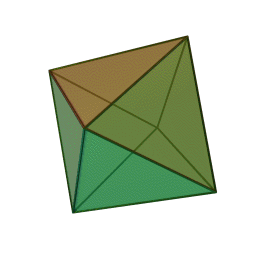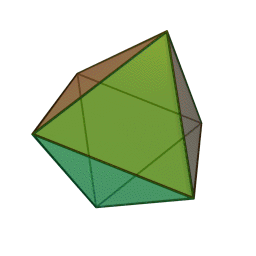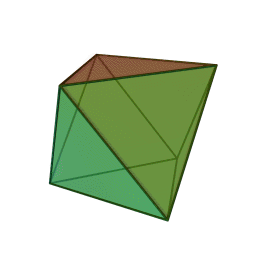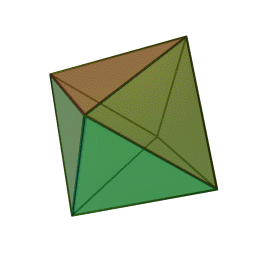
Сегодня общение абонента с банком или оператором мобильной связи происходит напрямую, без свидетельства третьего лица. Поэтому у абонента нет способа доказать, например, что он не заказывал тут или иную услугу, чем операторы активно пользуются.

Интересный вопрос - можно ли построить ограниченную сеть свидетельств так, чтобы каждая транзакция имела свидетеля, но общее количество задействованных участников было ограниченным.

И тут нам поможет тригонометрия! Вот замкнутые фигуры, состоящие из треугольников.

Тетраэдр

Октаэдр

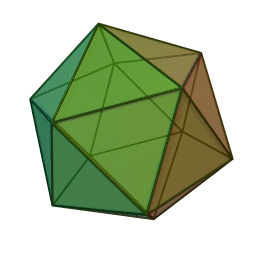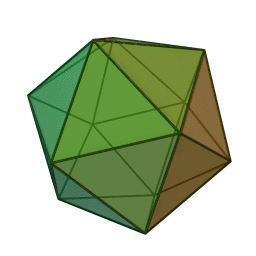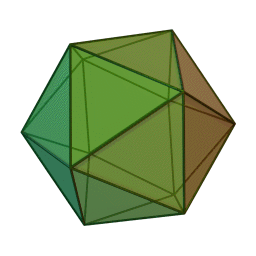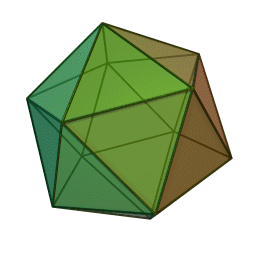
Икосаэдр

Построить замкнутую систему подтверждений можно при 4, 6, 12 участниках.